Two weeks ago, while waiting for my flight to San Francisco at an airport in Paris I stumbled on a coding challenge by NASA to optimize the solar arrays of the International Space Station. I’ll let the video explain:

Being very interested in Optimization for my soon-to-be-unveiled new startup, I was quite excited and promptly downloaded all the required material to spend my 10-hour flight hacking ;-)

The rules forbid talking about code while the contest is running but since it just finished, I would like to share how I built my solution with tools like OpenOpt, EC2 Spot Instances and MongoDB.

*Disclaimer: Shortly after landing I was the top Python solution and 10th overall but I couldn’t spend enough time on my code while abroad to stay that high in the charts. Final rankings are due this Friday so this is not a post describing the optimal solution but I hope it will be somewhat entertaining for Python coders and others. *

The contest

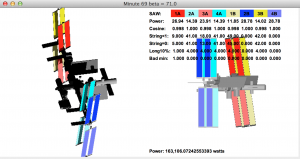
TopCoder made a Java simulator available along with the detailed description of the problem. The space station has 10 joints that can be rotated so all your program had to do was to output 10 angles and speeds for each of the 92 minutes of the ISS orbit, which would be visualized like this in the local tester:

The goal of the contest was to maximize the total power output of the station over the whole orbit (In the screenshot above I’m at 163kW on the 69th minute of the orbit) while respecting a couple of hard limits like the maximum speed & acceleration of each rotary joint, minimum power output for each panel and shadowed ratios on some parts like the longerons to avoid breaking due to heat expansion.

So the whole contest was basically about minimizing the shadows cast by the front solar arrays and the station itself.

My solution

TopCoder made the 3D model of the station available so theoretically (and that may be what the winner does) you could build an exact mathematical model of all the shadows and minimize that. However this was completely out of scope for my 10 hour flight so instead I decided to use a mixed approach based on both mathematical modelling and numerical optimization. The plan was to do most of the maths offline in the plane and then run a couple VMs over the following week that would optimize the parameters of my simplified model without oversight.

Pointing to the sun

Panels pointing to the sun

The first task was to align the panels at all time to the normal vector of the sun. That was made easy by the simulator that showed the viewpoint from the sun on the right. The hardest part there was to remember (or rediscover) all the formulas for cartesian/spherical conversions ;-)

One early optimization was to deviate from that sun angle so that the backpanels (in red) would have minimal shadowing. That was by far the most important gain and I built an almost-exact model of the sun angles on these panels to find the optimum (check nabuk’s schema).

Minimizing the station shadows

Worst position for station shadows

In order to point to the sun at all times, the panels have to do one full rotation per orbit (check the video at the end of this post). Which means that 2 times per orbit, a large part of the back panels will be heavily shadowed by the station. You can see on the right a screenshot at minute 82, one of the worst times of the orbit.

So the second biggest but perhaps most difficult gain was to accelerate the rotation of the panels when they were passing behind the station in order to minimize these bad angles.

There were 2 constraints: the hard limits on joint speed and acceleration, and the fact that any deviation from the “optimal” sun-pointing angle was reducing the potential power of the panels.

There was definitely a middle ground to be found between potential power and shadowing but given the complex shape of the station I wasn’t going to find it by an exact formula in a few days, let alone hours.

So I decided to approximate that function associating each angle with the optimal amount of deviation by numerical means, namely Global Optimization.

Enter OpenOpt

Python is one of my languages of choice not only because I love its syntax but because it has a mature ecosystem. Among the many availables modules are powerful scientific libraries like SciPy and OpenOpt.

OpenOpt is a suite of tools and optimization algorithms for solving both Linear and Nonlinear problems, supporting a large number of solver backends and (sometimes confusing) interfaces. There may have been better frameworks for my problem but I downloaded it in a rush just before my flight was departing as it seemed the most comprehensive and experimentation-friendly with its multiple algorithms.

Some optimization problems can make use of Vectorization, meaning that OpenOpt can build an internal model of their result function in order to speed up the process and make some assertions on the optimal result. However that is not the case for this problem: I had to consider the local ISS simulator as a black box that had about 92*20 input variables and one result, the total power output (which was the challenge score before maluses).

OpenOpt has several algorithms available for Global Optimization that can converge towards the best solution when there are many variables and multiple local optima. After some tinkering I settled on Differential Evolution (DE), a kind of genetic algorithm that was bundled in OpenOpt.

Parallelization

The biggest issue for this kind of numerical optimization was that the downloadable Java tester was very slow. Supposedly because it had to calculate all the exact shadows it took about 10 seconds to run on my MacBook Pro. Moreover, the contest specified 6 different beta angles which meant about 1 minute was required to evaluate the performance of one set of input values.

1 minute is an extremely high amount of time for algorithms like DE that require a large population of input candidates to be tested at each step of the evolution process. I guessed I would need about 6 (beta angles) * 50 (evolution steps) * 100 *(population size) ** 10 (different input sets) evaluations to have a good enough solution, which meant 35 days of my CPU time.

That was obviously not going to be possible so after landing I decided to launch about 50 EC2 spot instances where I could run DE in parallel, have them send the results to a free MongoHQ database and just merge them together before submitting my solution. Parallelization was made easier by the fact that there was several independent variables like the beta angle that could just be split among instances.

Spot Instances are great because they are often 10 times cheaper than regular ones. Their downside is that they can be terminated at any time by Amazon if their market price exceeds your initial bid but that wasn’t going to be an issue for this kind of computation. My final bill was about $50.

I want to pause there for a second and pay my respects to the AWS team that makes this possible. When you think about it, bidding for CPU time from your command line is insanely cool ;-) And when it’s for optimizing the space station, I guess that’s geek heaven.

Anyway, my biggest issue with Spot Instances was their launch time. You have to submit a bid that is evaluated for some time before AWS decides to allocate you the actual instances. That delay was at times as high as 10-15 minutes. I also ran into a known bug where the quota of spot instances wasn’t freed after them being terminated.

Putting it all together

There were a couple other numerical parameters (like station yaw) and approximations I optimized for in my solution but they yielded limited gains compared to the above.

This is a video of my solution for beta=75:

That’s it! I really enjoyed this challenge. The TopCoder rules were a bit weird at times but kudos to them and NASA for getting people involved and sharing some of their daily challenges. However I’m quite sure NASA has a whole team dedicated to this kind of optimizations and no significant improvement over their own solution will be made here, unlike the Netflix Prize.

I’m also sure I won’t be #1 but regardless, it was by far the coolest time I ever had on a plane ;-)