Working on the algorithm for Jamendo’s “similar albums”
I’m currently working on a big rewrite of the algorithms behind Jamendo’s “Similar albums”. The new algorithm will focus only on tags because there will be both “Similar albums” and “Related albums” (where I’ll put recommended stuff). I was really slow this morning while thinking about it so I decided to blog the whole process in real time ;-)
Let’s begin! The problem is, we have a list of weighted tags for each album and we want to compute for each album the list of album that have the most similar tags list.
Here is a sample tag/weight list for the Manu Cornet album:
jazz 19.8494 latino 18.4662 bossa 16.4924 contrebasse 16.4924 sensible 16.4924 world 16 basse 15.6844 hamonica 15.6844 batterie 15.6844 tamtam 15.6844 improvisation 15.6844 piano 8.48528 easylistening 7.34847 ambient 6.63325
Let’s call this base album “A1” and the similar albums we’re looking for “A2”. We can consider that “20” is the maximum tag weight.
A quick list of requirements for the algorithm :
- Shouldn’t be symmetric
- Should penalize A2s if they lack one or more of the most important tags of A1
- Should be quite fast, even if we’re not going to run it on the fly (everything will be computed once a day)
Martin told me yesterday about the nice app “Grapher” which is bundled with OS X. I’m going to use it to write the formula.
My first idea was, for each tag of A1, to compute a number Z between -1 and 1 and add them all. Let (x,y) be the weight of the tag in A1 and A2 respectively. The most obvious algorithm would be :
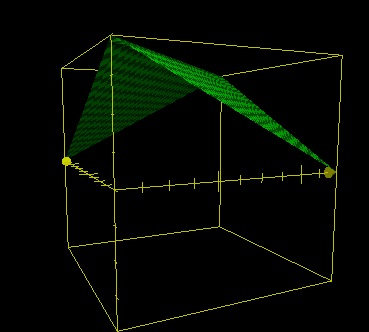 z=20-ABS(x-y)
z=20-ABS(x-y)
The axis on the left is Y, on the right it’s X and the elevation is of course Z. The window is (0,20),(0,20),(-20,20)
Easy improvement : multiply by x/20
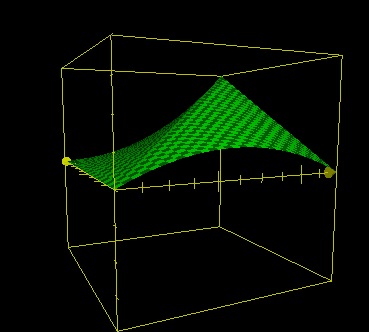 z=(20-ABS(x-y))*x/20
z=(20-ABS(x-y))*x/20
Quite good but there is a problem over the X axis. If y=0, z should always be < 0. Another easy solution : add min(0,y-x)
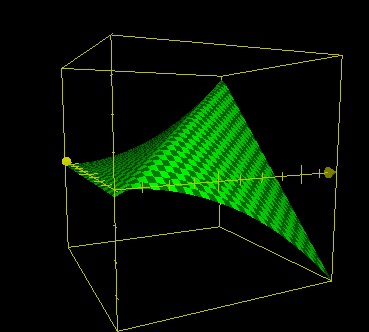 z=(20-ABS(x-y))*x/20+min(0,y-x)
z=(20-ABS(x-y))*x/20+min(0,y-x)
New problem : x=20, y=10. In these conditions z shouldn’t be nul. Let’s multiply min(0,y-x) by (1-y/20).
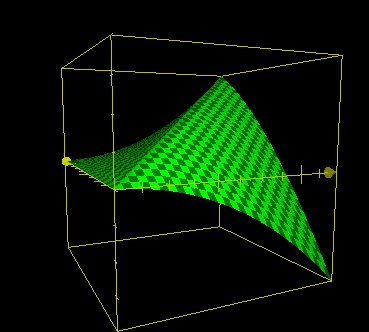
z=(20-ABS(x-y))*x/20+min(0,y-x)*(1-y/20)
Better, but not good enough yet. (1-y/20)^4 ?
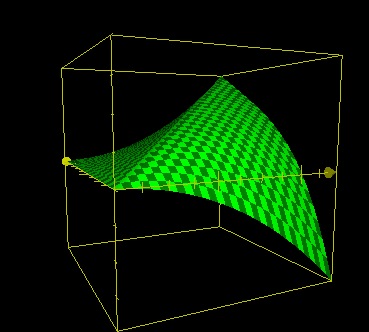
**z=(20-ABS(x-y))\*x/20+min(0,y-x)\*(1-y/20)\^4**
Well, it looks quite good to me! Maybe we could tweak some curves a bit but let’s go for this one for now.
Here are the results for the Manu Cornet album :
id weight_sum ----------------------- ------------------ 2336 89.7347740595245 608 84.9463957742962 2013 79.2737167470594 2239 78.7533019317343 1968 78.3494367998522 3552 78.2419321761695 2626 77.4643574361218 868 76.3107863971299 (query took 1.2 seconds)
I am not so happy with the results. Maybe there need to be another negative zone for tags that are in A2 but not in A1 after all.
Let’s reduce the window size to (0,1),(0,1),(-1,1) and take those “20” factors out. Now much easier, here is what I’ve come up :
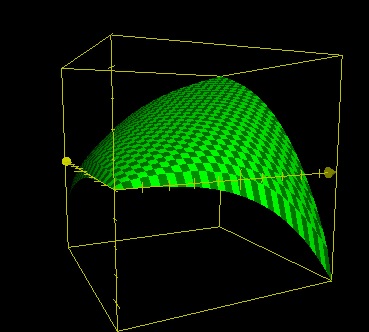
z=SQRT(x*y)+MIN(0,(y-x)^3)+0.5*MIN(0,(x-y)^3))
Looks good too but let’s compare the results :
id weight_sum ------ ------------------ 608 4.49465968951514 2336 4.32499417058527 2013 3.74828022088347 3552 3.49127205825584 2626 3.44471851383391 2407 3.35824086666307 2239 3.3511421181151 1968 3.27891762132192 868 3.18629627915296 1013 3.18123969513814 1741 3.11171873935927 (query took 1.2 seconds)
Quite funny that both queries take the same time to process: the formula doesn’t seem to be the bottleneck. Results are a bit better but I think there will still be some tweaking needed in the future. Maybe reduce the negative zones.
Anyway, now I’m going to implement this and the new data should be online in a few minutes. Don’t forget to check out the “Similar albums” slider on your favourite albums pages!